فرمول های پاره خط و نیم خط
1-هرگاه چند نقطهی متمایز(جدا از هم)،بر روی یک خط راست باشند تعداد پاره خط ها از فرمول زیر به دست می آید.
2 ÷ (تعداد فاصله ها × تعداد نقطه ها ) = تعداد پاره خط ها
توجه : تعداد فاصلهها همیشه یکی کمتر از تعداد نقطهها است.
2-هرگاه چند نقطهی متمایز،بر روی خط راست باشند، تعداد نیم خطها از فرمول زیر،به دست می آید.
2 × تعداد نقطهها = تعداد نیم خطها
3-هرگاه چند نقطهی متمایز، برروی یک نیم خط باشند،تعداد نیم خطها مانند مثال زیر به دست میآید.
مثال: برروی یک نیم خط،هفت نقطهی متمایز وجود دارد چند نیم خط،در شکل وجود دارد؟
پس (8 = 1 + 7 ) نقطه داریم یعنی 8 نیم خط خواهیم داشت.
4- هرگاه چند نقطهی متمایز، برروی یک پاره خط باشند نیم خطی، درشکل وجود ندارد.
برش و قسمت:
وقتی
می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی
تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
مجموع و اختلاف:
هرگاه مجموع دو عدد و اختلاف آن دو عدد را به ما بدهند و آن دو عدد را از ما بخواهند، از دو راه زیر به دست میآید.
1-اگر مجموع واختلاف را از هم کم کرده،بر2 تقسیم کنیم عدد کوچکتر به دست میآید.
2- اگر مجموع واختلاف را با هم جمع کرده،بر2 تقسیم کنیم عدد بزرگتربه دست میآید.
تعداد یک رقم در یک مجموعهی اعداد متوالی
1-از عدد1 تا 99 از همهی رقمها 20 تا داریم به جز رقم(صفر)،که از آن 9 تا داریم.
2-از عدد 100تا 199 از همهی رقمها 20تا داریم به جز رقم(یک)،که از آن 120 تا داریم.
3- از عدد 200تا 299 از همهی رقمها 20تا داریم به جز رقم(دو)،که از آن 120 تا داریم و ...
تعداد اعداد
در
مجموعه اعداد طبیعی (از یک شروع میشود)تعداد اعداد یک رقمی9 تا،اعداد دو
رقمی 90تا،اعداد سه رقمی 900تا،اعداد چهاررقمی 9000 تاو... می باشد.
تعیین تعداد عددهای صحیح یک مجموعهی اعداد متوالی
1-اگر تعداداعداد،از عدد اولی تا عدد آخری مورد نظر باشد از فرمول زیر،استفاده میشود.
1 + (عدد اولی – عدد آخری) = تعداد اعداد
مثال: از عدد27 تا عدد 1027 چند عدد صحیح (عددی که کسری و اعشاری نباشد) وجود دارد؟
تعداد اعداد 1001 = 1+(27 – 1027 )
2-اگر تعداد اعداد،بین دو عدد اولی و آخری مورد نظر باشد از فرمول زیر،استفاده میشود.
1 – ( عدد اولی – عدد آخری) = تعداد اعداد
3- اگر تعداد اعداد زوج و یا فرد یک مجموعهی اعداد متوالی مورد نظر باشد از فرمولهای زیر استفاده میشود.
1+ 2÷(کوچکترین عدد زوج – بزرگترین عدد زوج) = تعداد اعداد زوج
1 + 2÷(کوچکترین عدد فرد – بزرگترین عدد فرد) = تعداد اعداد فرد
مثال: از عدد 45تا 158چند عدد زوج وچند عدد فرد وجود دارد؟
57= 1 + 2 ÷ (46 – 158 ) = تعداد اعداد زوج
57 = 1 + 2 ÷ ( 45 – 157 )= تعداد اعداد فرد
------------------------------------------------------------------------------------------------------------------------------------------------------------
مجموع اعداد صحیح متوالی
1-برای محاسبهی مجموع اعداد صحیح متوالی،از فرمول زیر استفاده میشود.
2 ÷ (تعداد اعداد × مجموع عدد اولی وعدد آخری ) = مجموع اعداد صحیح متوالی
مثال: محموع اعداد صحیح از 1 تا 100 را به دست آورید؟
مجموع اعداد 5050 = 2 ÷ 100( × (100 + 1 ))
2- برای محاسبه مجموع اعداد صحیح فرد متوالی که از عدد(یک) شروع
میشوندویا مجموع اعداد صحیح زوج متوالیکهازعدد(دو)شروع میشوند
علاوه بر فرمول قبلی،میتوانیم از فرمول های زیر استفاده کنیم.
تعداد اعداد × تعداد اعداد = مجموع اعداد صحیح فرد متوالی
(1 + تعداد اعداد) × تعداد اعداد = مجموع اعداد صحیح زوج متوالی
مثال: مجموع اعداد صحیح زوج و مجموع اعداد صحیح فرد متوالی از 1 تا100 را به دست آورید؟
از 1 تا 100 ، 50تا فرد و 50 تا زوج هستند.
2500 = 50 × 50 = تعداد اعداد صحیح فرد متوالی
2550 = 51 × 50 = تعداد اعداد صحیح زوج متوالی
عدد وسطی
هرگاه
مجموع چند عدد صحیح متوالی (با فاصله های یکسان) را بدهند و آن اعداد را
بخواهند ،مجموع آن اعداد را بر تعدادشان تقسیم کرده،عدد وسطی به دست
میآید.
1- اگر تعداد اعدادفرد باشد مانندمثال زیر عمل،می کنیم.
مثال: مجموع 5 عدد صحیح متوالی 75 میباشدکوچکترین عدد را به دست آورید؟
عدد وسطی 15 = 5 ÷ 75
75 = 17 + 16 + 15 + 14 + 13
2- اگر تعداد اعداد زوج باشد مانند مثال زیر عمل می کنیم.
مثال: مجموع 6 عدد صحیح فرد متوالی 96 می باشد یزرگ ترین عدد را به دست آورید؟
رقم یکان
1- هرگاه چند عدد زوج را با هم جمع کنیم رقم یکان حاصل جمع،حتماً زوج خواهد شد.
2- هرگاه چند عدد فرد را با هم جمع کنیم رقم یکان حاصل جمع،ممکن است زوج باشد یا فرد.
اگر تعداد اعداد،فرد باشد رقم یکان حاصل جمع،فرد میشود و بلعکس
3-هرگاه عدد زوجی را هرچند بار در خودش ضرب کنیم رقم یکان حاصل ضرب،حتماً زوج خواهد بود.
کسر بین دو کسر
برای نوشتن کسر بین دو کسر،کافی است صورتها را با هم و مخرجها را نیز را باهم جمع کرد به مثال زیر توجه کنید.
سه کسر بین دو کسر نوشته شده است.
بخش پذیری
بخش
پذیری بر 11 : از سمت چپ شروع می کنیم و ارقام را یکی در میان با هم جمع
می کنیم و بعد حاصل را از هم کم میکنیم و حاصل تفریق را بر 11 تقسیم
میکنیم،اگر باقی مانده صفر شود بر 11 بخش پذیر است.
مثال: آیا عدد 32121456 بر 11 بخشپذیر است؟
تقسیم کسرها:
تقسیم کسرها را به سه روش زیر، می توانیم انجام دهیم.
1- اگر مخرجها مساوی باشند از مخرجها صرف نظر کرده صورت کسر اول را بر صورت کسر دوم تقسیم میکنیم.
اما اگر مخرجها مساوی نباشند مخرج مشترک گرفته و مخرجها را مساوی میکنیم سپس صورت کسر اول را بر صورت کسر دوم تقسیم میکنیم.
2- کسر اول را نوشته، علامت تقسیم را به ضرب تبدیل کرده و سپس کسر دوم را معکوس می کنیم و عمل ضرب را انجام می دهیم.
3- دور در دور و نزدیک در نزدیک: از این روش، فقط در مواقعی که لازم باشد استفاده می کنیم.
نسبت و تناسب :
1- تناسب زمانی : در این نوع تناسب، زمان تغییری نمی کند.
مثال : اگر 4 پیراهن روی طناب در مدت زمان یک ساعت خشک شوند 8 پیراهن در همان شرایط در همان یک ساعت خشک می شود.
2-
تناسب مستقیم : اگر قیمت یک تخم مرغ 100 تومان باشد 5 تخم مرغ 500 تومان
می شود یعنی با افزایش تعداد تخم مرغ ها، قیمت خرید تخم مرغ ها نیز به
همان نسبت افزایش می یابد.
3-
تناسب معکوس : گاهی اوقات کمیت ها با هم نسبت عکس دارند یعنی هرچه یکی را
زیاد کنیم به همان نسبت ، دیگری هم کم می شود. در این حالت می گوییم تناسب
معکوس است. مثلاً اگر2 کارگر، کاری را در مدّت 6 روز انجام می دهند ،4
کارگر، همان کار را در مدت 3 روز انجام می دهند.
زاویهی بین دو عقربهی ساعت شمار و دقیقه شمار:
برای
محاسیه زاویهی بین دو عقربهی ساعت شمار و دقیقه شمار ، مقدار ساعت را در
عدد 30 ضرب کرده، مقدار دقیقه را در عدد5/5 ضرب کرده، عدد کوچک تر را از
عدد بزرگ تر کم می کنیم. در صورتی که جواب به دست آمده از 180 درجه بیشتر
باشد آن را از 360 کم می کنیم.
مثال: زاویه ای که دو عقربه ی ساعت شمار و دقیقه شمار در ساعت 1:50 می سازند چند درجه است؟
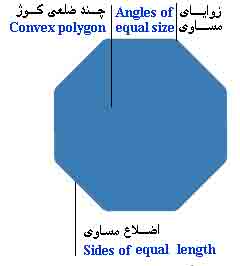
مجموع زوایای داخلی چند ضلعی ها:
برای این که مجموع زاویه های داخلی هر چند ضلعی رامحاسبه کنیم ، تعداد ضلع ها را منهای 2 نموده ، در 180 ضرب می کنیم.
180 × (2 – تعداد ضلع ها ) = مجموع زاویه های داخلی
مثال : مجموع زاویه های داخلی یک 5 ضلعی را به دست آورید؟
درجه 540 = 180× (2 – 5 ) : پنج ضلعی
تعداد قطرهای چندضلعی ها:
از تعداد ضلع ها، 3 تا کم کرده، جواب را در تعداد ضلع ها ضرب کرده و سپس جواب را بر 2 تقسیم می کنیم.
2÷ تعداد ضلع ها × ( 3 - تعداد ضلع ها ) = تعداد قطرها
از هر راس چند ضلعی به اندازهی (3- تعدا ضلع ها ) قطر می گذرد. مثلا از یک راس چهار ضلعی ( 1= 3 – 4) یک قطر می گذرد.
مثال : یک شش ضلعی چند قطر دارد؟
تعداد قطرها 9= 2 ÷ 6 × ( 3 – 6 )
تعداد زاویه ها:
هرگاه در چند زاویه ی مجاور که دارای راس مشترک هستند ، بخواهیم تعداد زاویه ها را تعیین کنیم ، از فرمول زیر استفاده می کنیم.
2 ÷ (تعداد فاصله ها× تعداد نیم خط ها ) = تعداد زاویه ها
توجه : تعداد فاصله ها،از تعداد نیم خط ها یکی کم تر است.
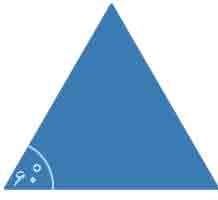
مثال : در شکل روبرو چند زاویه وجود دارد؟
ارتفاع وارد بر وتر:
برای محاسبه ارتفاع وارد بر وتر ، می توانیم از فرمول زیر استفاده کنیم.
وتر ÷ حاصل ضرب دو ضلع زاویهی قائمه= ارتفاع واردبر وتر
مثال : اگر دو ضلع زاویهی قائمه مثلث قائم الزاویهای 5 و 12 س باشدووتر آن 15 س باشد.طول ارتفاع وارد بر وتر آن چقدر است؟
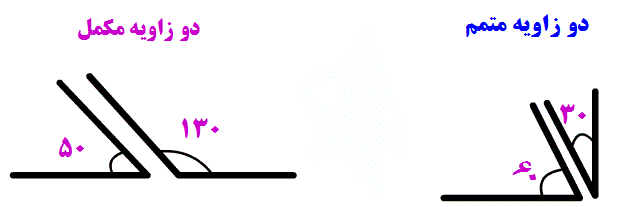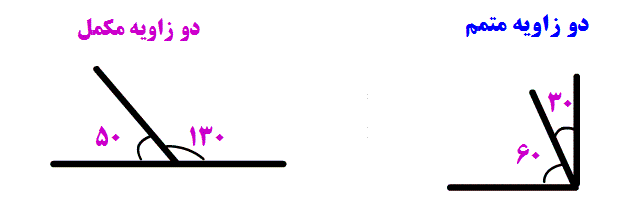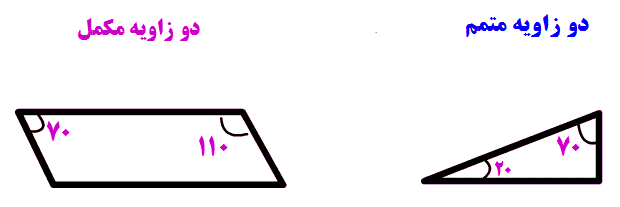
دانش آموزان را باید با اهداف آموزشی و روشهای جدید آشنا کرد در این زمینه فعالیت مان را آغاز کردیم شاید قدم کوچک ما آغاز بزرگی برای شما باشد.